







Philosophically, people have attempted to bridge our sense of beauty, harmony and rhyme and reason, with universal structure, geometry and understanding, in what could be described as a quest to understand our reality and ourselves, with the expression of our musical structure and harmony being a direct reflection of that.
Currently there are many interpretations of musical structure that reflect the culture in which it was developed, but by far the most widely adopted system is 12 tone equal temperament, a division of the octave into 12 equally proportioned intervals, based not of pure harmonic relations, but for the sake of balancing out of dissonances that occur between certain pure notes for the greatest flexibility of musical expression, at the expense of these pure intervals.
Phi, also known as the golden ratio or more provocatively, the divine proportion, is well known for its Special properties, both from a mathematical and artistic perspective. From the natural spirals of plants, shells, and galaxies to the proportions of our own human form, many would say there is a convergence of nature and the universe toward this mathematical principle, a bold claim others would also dispute.
This begs the question, can we create a system of musical tuning that aligns with natural geometry while also remaining consonant? Could we map musical symphonies to the spiral seeds of the sunflower and create a marriage of harmony, beauty and a mathematical order expressed by nature?
Briefly, we first need to understand the basic theory of what constitutes a consonant musical interval. Basically, an object will have a fundamental frequency with a corresponding harmonic series, with the harmonics in the harmonic series being represented in their position by any whole number multiplication of the fundamental frequency.
The sequential relationship between these harmonics in order, represent the mathematically harmonic intervals. the first harmonic is equal to F x 2 or 2 : 1, known as the octave and most consonant interval, exhibits the phenomenon of “octave equivalence” in which we audibly perceive all notes an octave apart to be the same note. One step further from the octave is the second harmonic and their relationship is known as a “fifth” or 3 : 2, and the next most consonant interval. As we continue this pattern we get to the “fourth” or 4 : 3 then the major third, 5 : 4 and the minor third 6 : 5. We can see that basically the simpler the ratio between the frequencies, the more consonant we tend to perceive them as musical intervals.
By Cree M.J.


The Romanesco broccoli is a natural hybrid of broccoli and cauliflower.
Phi ratios or derivatives are often associated with the spirals of seashells.

The Harmonic Series


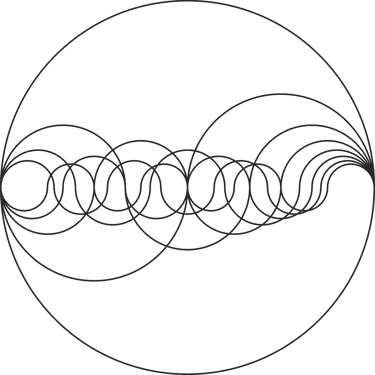
The Octave 2:1, its phenomenon of "octave equivalence" becomes poetically visible as a series of fractal-like yin-yangs in the harmonic series when only the octave is drawn out.
2:1
4:2
8:4
16:8
32:16
Mirrored
Preamble
As would be expressed by a single string


Fifth 3:2
Fourth 4:3
Major Third 5:4
Minor Third 6:5
7:6
8:7
The principle of octave equivalence to create the relationships between intervals, is intuitively a simple basis for a consonant musical structure, for harmonies to span as wide a pitch spectrum as possible.
With the harmonic intervals in mind, it might be hard to conceive that Phi with its ratio of 1 : 1.61803398... could create pleasant sounding musical intervals, and in one sense Phi could be described as the MOST irrational number, which directly clashes with the principle that consonant intervals are based on simple ratios.
As we can see the consecutive ratios of the harmonic series creates this interesting "wiggling tadpole" pattern. While resonating systems will oscillate in a sine wave pattern rather than semi circles, the sine wave pattern can also be attributed to the path of any given point on a rolling circle, thus a sine wave is effectively mapping the motion of a circle and one peak or trough of a sine wave could be attributed to a semi-circle, at least in an illustrative sense.


2:4:8:16
The nature of the overtones of any given musical device also will influence what exactly sounds in tune, with the harmonic series mainly pertaining to string and wind instruments, where natural harmonics are not out of their natural sequence, a metal bells particular shape can often shift the overtones.
Sine Octave Series