
By Cree M.J.
The Phionic Series
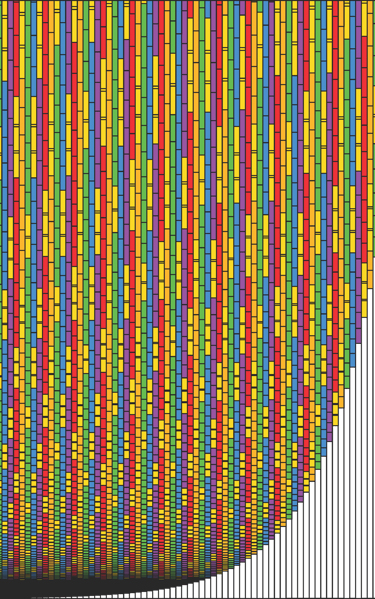
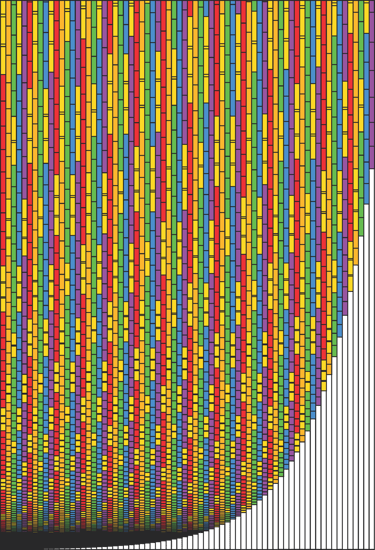
The expanded chart of the Phionic series reveals an interesting pattern of sweeping bridge intervals. We may question exactly what its significance is and how can it be utilised as a polytonal model.
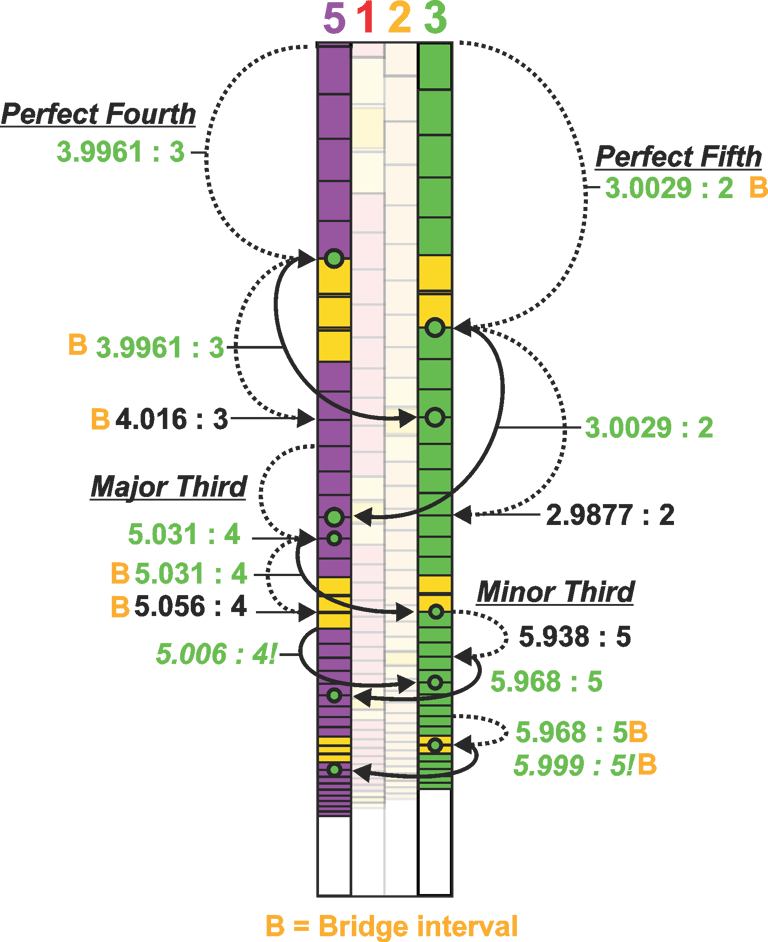
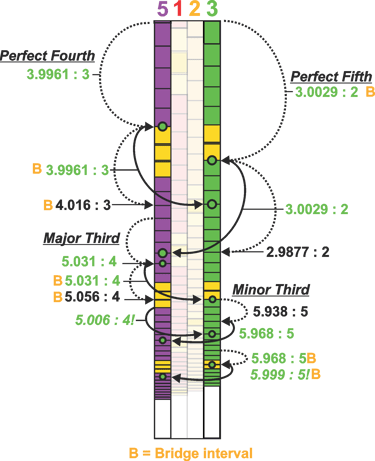
One potentially interesting way to utilize the multiple scales of the Phionic Series is to take advantage of the Bridge Interval across multiple scales. Relative to the central Scale Three, the scales three steps above or below that begin the next Phi-cycle exist in an overall ratio of approximately 4.016:3, which is close to a perfect fourth between the fundamental octaves.
By aligning the nearest corresponding intervals, or by observing Bridge alignments, we can see that the closest intervals between these scales are separated by a precise ratio of 1:1.00507 — the difference between the Bridge Interval and the standard interval.
Through creative use of two scales, or by transiently shifting between them, it becomes possible to take advantage of the favorable intervals of the Phionic Series. In practice, this implies only a very small change in key: essentially a shift of the entire system by a fixed ratio of 1:1.00507.
These scales could also be played simultaneously in what could be considered a "coupled" relationship, to create what is similar to a chorus effect, but not with a typical arbitrary detuning. Instead in an interlocking relationship of harmonic ratios and intervals.
This creates a unique opportunity for acoustic instruments with multiple strings or courses played together, such as the twelve-string guitar, piano, mandolin, lute, and dulcimer.
By tuning the individual strings within each course to two different scales in a type of polytonal tuning, it becomes possible to create a transient tonal centre and harmony, this involves the simultaneous presence of both the Bridge Interval and the standard interval at all locations.
This produces a situation where, for any given interval, at least one string is as closely in tune as possible within the Bridge Interval system. As both scales are played simultaneously, they interchange between providing the leading consonance and complimenting the other.
Because our brains a programmed to recognise harmonic intervals, the usual phenomenon of beating where we hear an in between tone is cancelled out, and our brain perceives the most in tune note as the tonal centre.
In effect, One note will always be slightly more consonant than equal temperament, and because a new interval condition is created by using two scales and bridges, some intervals will be very close approximations of just intonation.
This Phionic Polytonal tuning possibly contains more consonant harmonic ratios than any other tuning system described, with the caveat of sounding richly ethereal.
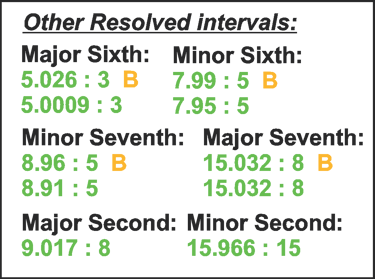
Octave - 2 : 1 Perfect Fifth - 3:0029 : 2 Perfect Fourth - 3.996 : 4
Major Third - 5.006 : 4 (New) Minor Third - 5.999 : 5 (New)
Major Sixth - 5.0009 : 3 (New) Minor Sixth - 7.99 : 5 (New)

In the context of microtonal music, we can experiment with using two or more different scales to access unique combinations of intervals that may not be available within a single scale, and even achieve intervals that are more harmonically in tune or unique across scales.
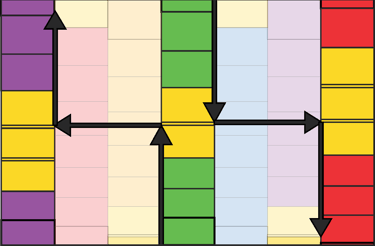
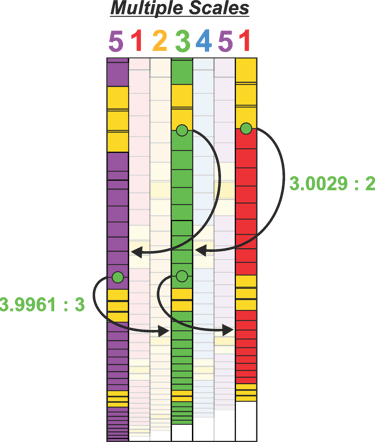
Because all of the scales are geometrically fixed, we can identify between which scales a specific interval most accurately lies, as well as the conditions that align with it. We can also observe that, if we were to avoid crossing the Bridge Interval and instead continue increasing the smaller ratio, we would at the point of the Bridge, effectively “jump” into another scale.
For example, if we begin on Scale Three and ascend note by note toward the Bridge without crossing the Bridge Interval, we eventually arrive at Scale Five of the previous Phi-cycle. The inverse is also true: if we descend and do not cross the Bridge Interval, we will arrive at Scale One of the next Phi-cycle. (Phi cycles are explained in "Phionic Geometry")
If we analyze the positions of the Bridges, we can observe both a horizontal ascending pattern and a vertical sweeping curve. We can also see that consecutive Bridges in this pattern align with other Bridges along the series. A Bridge occurs every three steps horizontally, with fifteen steps between the middle scales, crossing the Bridge of each different scale before returning back.