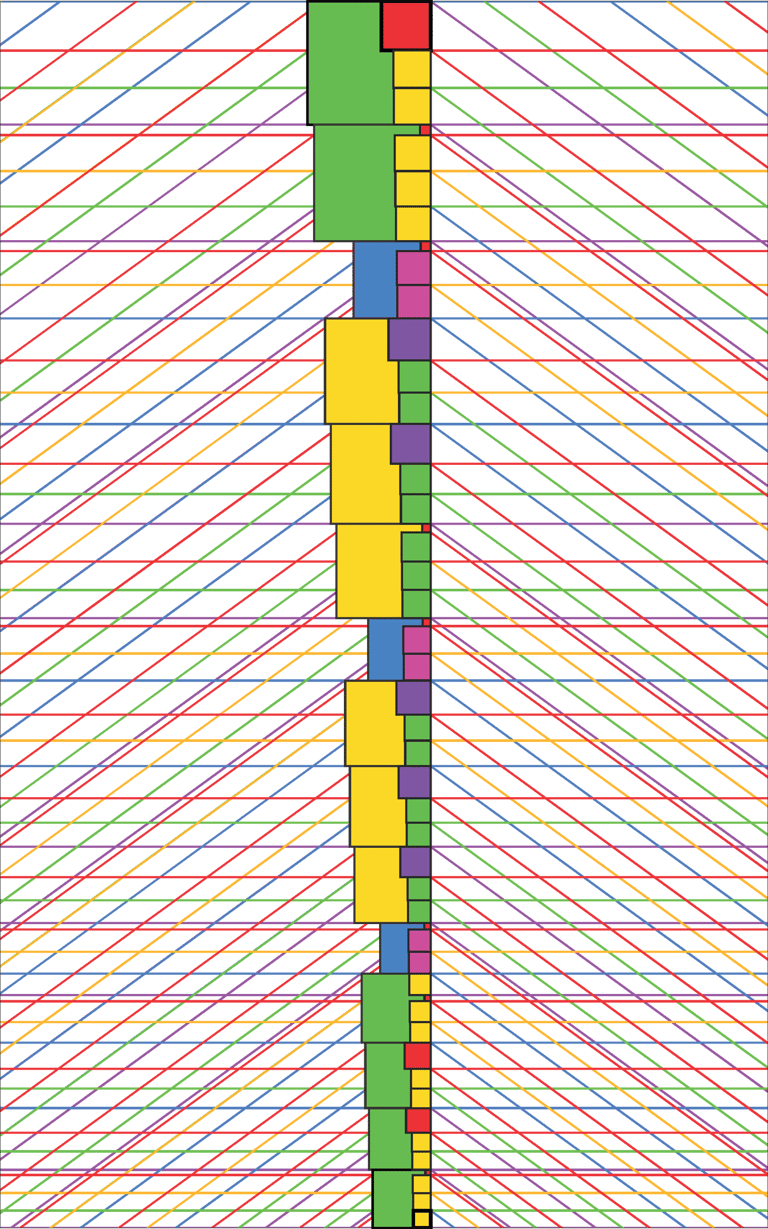
By now, we have completed five iterations of our first basic structure, which together yield the same values we would reach by simply continuing to multiply and divide the original octaves by Phi in three cycles of 13. In the following process, we can demonstrate how these five iterations correspond to particular Phi-harmonic nodes and points of interrelation within the overall structure.

The next step is to overlay the five iterations and highlight the intervals naturally created by each, relative to its own iteration. By examining the base intervals of one iteration in the context of the interpenetrating intervals from the other four iterations, we generate a series of sub-intervals from the perspective of each unique iteration.

By Cree M.J.

Phionic Geometry

The Connected Whole

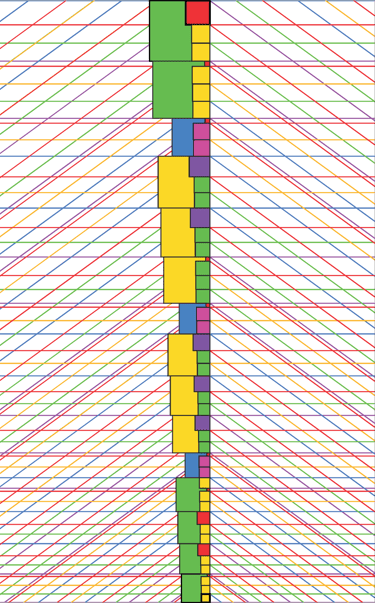
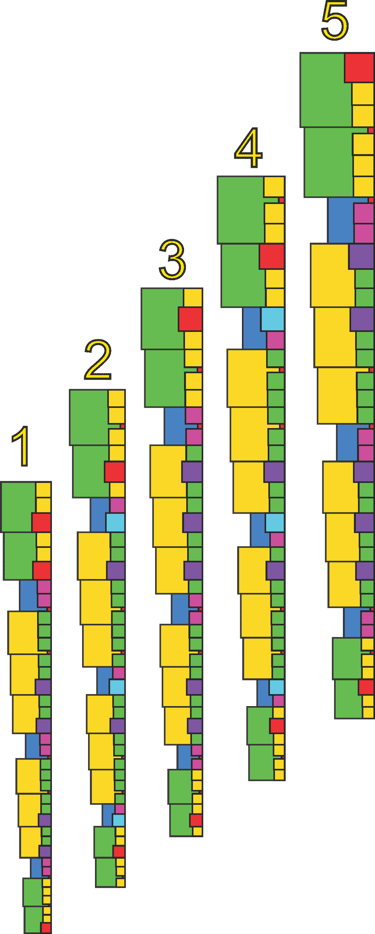
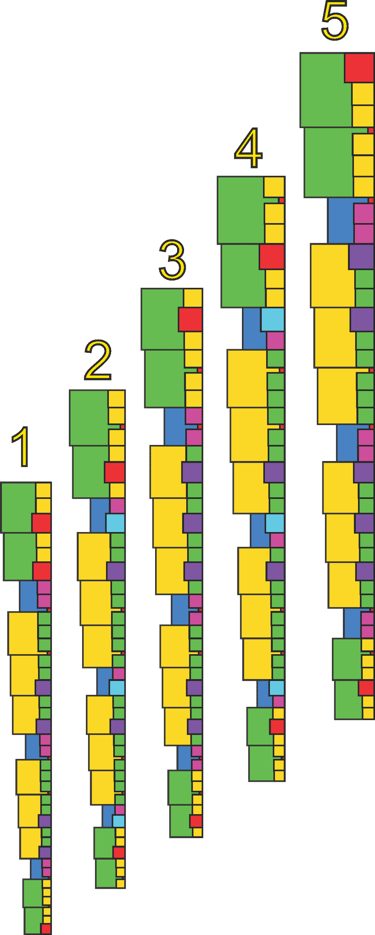
Now we can see a complex relationship of intervals across the 5 iterations. Though the literal values of each interval remains constant , relative to each set, it has a different framework to work with.

There is now only one final step to reveal the structure. We take the musically familiar 1:1.059 ratio present within the iterations and use it to construct an entirely new scale, assigning each note to the closest available interval within the existing iteration values.

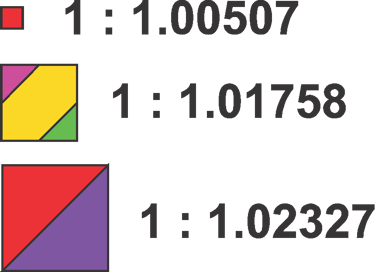
Because our interval is slightly less than the 12th root of 2 (1:1.05946), the standard interval of equal temperament, a small discrepancy remains, and the 1:1.059 ratio falls just short of completing the octave. This new interval is not an unfortunate inconsistency; rather, it reflects the interrelations of the iterations, the Phi organizing principle, and the phase-in/phase-out points between iterations. This interval may be referred to as the “Bridge Interval.”

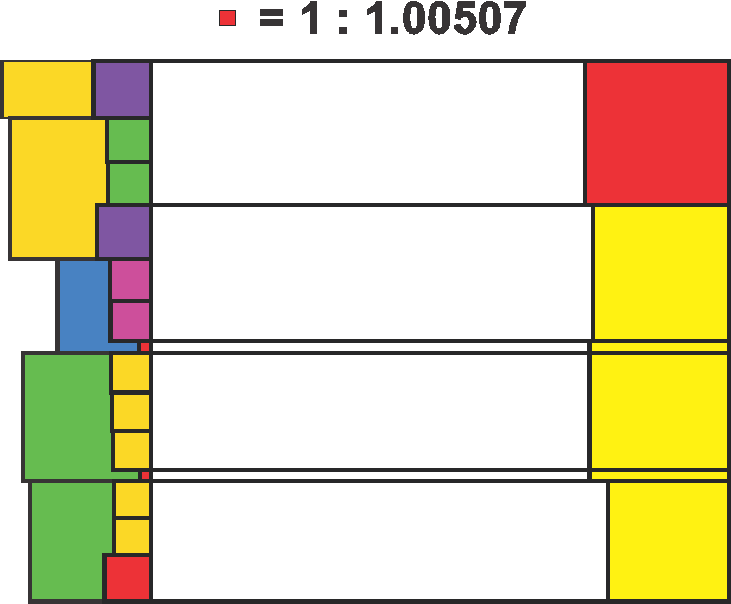
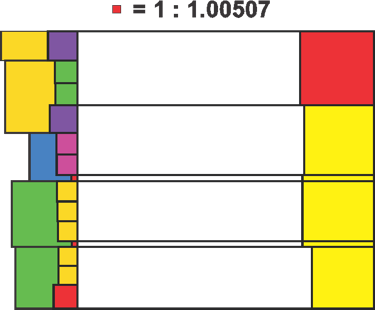
Comparing the five Phionic scales, we see that the first is equivalent to the fourth, and the second is equivalent to the fifth, effectively reducing the structure to three unique scales. The central scale is uniquely stable, with only two possible Bridge Interval locations. When we compare these three scales to the five iterations, we find that every interval has been efficiently assigned without overlap, forming a series of consonant scales determined solely by the Phi organizing mechanism.

This completes the Phionic structure—a system that can be understood as the musically consonant harmonic nodes of a series of golden ratio-based octaves. It describes not just a single scale, but a unified field of interwoven scales.

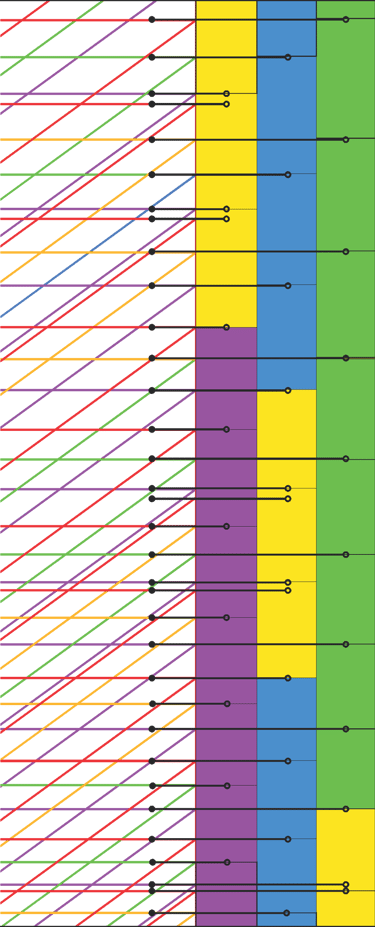
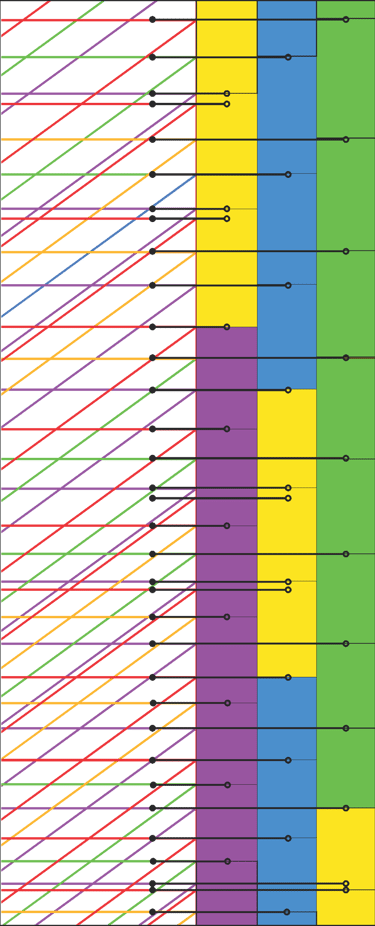
Now that we have identified the core of the Phionic Series, we can expand the scale to reveal an endless chart of possible Phi-Octave relationships. This series is intended for musicians interested in exploring tuning based on the golden ratio, offering a geometric, poly-scale, microtonal framework of intervals.

Now, the Bridge Interval follows a clear sweeping path through the iterations, a consequence of the Phi organizing mechanism. Within the iterations, this interval arises as the structure breaks down into smaller intervals for a second time—the first breakdown occurring in the ratios of the three cycles of thirteen, or five iterations. Because Phi is irrational, these cycles do not have well-defined starting or ending points, and the structure begins to break down at the combination of the first and last iteration of a cycle.

Thus, the Bridge Interval can be seen as the point where the structure spans the gap between the first and last iteration. The exact nature of this dynamic becomes clearer when we identify the iterations from which each interval is derived. A distinct gradient pattern emerges: the scale draws intervals from each iteration in an ordered sequence, moving down through the iterations as the octave ascends, or up through the iterations as the octave descends, guided by the Bridge Interval. This pattern is consistent across all five scales. With these insights, we can understand that our original scale was not merely a series of randomly detuned clusters, but rather a segment of a larger, harmonically coherent structure.

While the 1:1.059 ratio intervals remain consistently connected across the system, the Bridge Interval locations are not fixed. If we were to shift our octave points upward by a 1:1.059 ratio, we would maintain the same 1.059 intervals, but the Bridge Interval positions would shift accordingly. From this, we can understand the Bridge Intervals as waves propagating through the system—not as fixed points, but as relative positions that cycle back after one octave.

After completing this process, we find that Iteration 1 and its sub-intervals have three possible locations for the Bridge Interval, all situated near the bottom of the octave. This effectively expands the potential notes in the scale from 12 to 14. With this understanding, we can proceed through the five iterations and map out the specific scales that are generated.

If we sweep through the scale to determine where the Bridge Interval can be placed, we find that only certain locations are permissible. Specifically, these locations occur wherever a newly created interval in the scale lies adjacent to the smallest sub-interval, 1:1.00507. This sub-interval results from the overlap of the first and last iterations, completing the Phi-Cycle and “spilling over” into the next series of divisions.